Calcolare la lunghezza di un segmento su un piano cartesiano, la distanza tra due punti
Per calcolare la lunghezza di un segmento AB, ossia la distanza tra i punti $A$ e $B$ posso usare il teorema di Pitagora, prendendo in considerazione i valori di A e B sugli assi delle ascisse e delle ordinate.
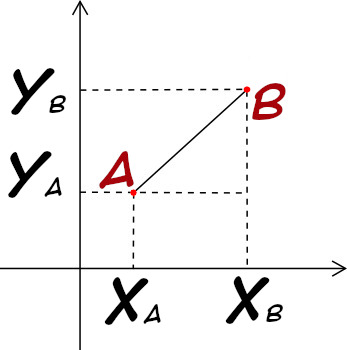
\(AB = \sqrt{(x_A-x_B)^2+(y_A-y_B)^2}\)
Nota: otterremo lo stesso risultato con A e B invertiti, siccome con l’esponente pari la distanza ottenuta è sempre positiva.
\(AB = \sqrt{(x_B-x_A)^2+(y_B-y_A)^2}\)
Ci sono anche alcuni casi particolari, che possono semplificare il calcolo:
- Se \(x_A = x_B \Rightarrow AB = \|x_B - x_A\|\)
- Se \(y_A = y_B \Rightarrow AB = \|y_B - y_A\|\)
Da non confondere con la distanza di un punto da una retta.
Formula menzionata in
Esegui una ricerca:
Caricando la sezione dei commenti, quindi cliccando il pulsante soprastante, accetti la politica sulla privacy di graphcomment e googletagmanager. Per più informazioni, clicca qui.
Un pratico grafico relazionale contenente tutte le formule di questo sito ed i collegamenti tra esse.